Using row and column operations to calculate determinants

For some special square matrices, determinants are relatively simple to calculate.

The determinant of a diagonal matrix is the product of the numbers down its main diagonal.

Proof: All elementary products of a diagonal matrix except the product of the numbers down the main diagonal must contain a zero.

We can make this more general.

The determinant of a triangular matrix is the product of the numbers down its main diagonal.

Proof: Suppose the matrix is upper triangular. Look for ways you can get a non-zero elementary product. You must take a number from each column.

For column 1, the only possiblilty is the first number.

From column 2, you can't choose the first number, since you already chose the first number in column 1, so you must choose the second number.

And so on: the only way you can get a non-zero elementary product is to take the product of the numbers down the main diagonal.

For a lower triangular matrix, look at which rows you can choose your numbers from.

This raises an interesting question: since you know how to use row operations to reduce a matrix to row-echelon form (which is upper triangular), can you use row operations to evaluate determinants? The answer: yes, if you're careful. Row operations change the value of the determinant, but in predictable ways. If you keep track of those changes, you can use row operations to evaluate determinants.

Elementary row operation	Effect on the determinant
Ri ↔ Rj	changes the sign of the determinant
Ri ← cRi, c ≠ 0	multiplies the determinant by c
Ri ← Ri + kRj, j ≠ i	no effect on the determinant
Proof: Omitted. (Uses the formal definition of the determinant).

So as long as you keep track of the effects of the row operations you use, you can reduce your matrix to triangular form and then just calculate the product of the numbers down the diagonal.

An example. Suppose you want to evaluate the determinant

You notice that row one has a factor 2, so you want to apply the row operaton R1 ← (1/2)R1. Doing so will multiply the determinant by 1/2, so you need to include an extra factor 2 to compensate.

Now you want to use row 1 to remove the 1's in column one of rows two and three. You use the row operations R2 ← R2 – R1 and R3 ← R3 – R1, which don't change the value of the determinant.

You want a non-zero as the leading element of row two. You decide to swap rows two and three: R2 ↔ R3, which will change the sign of the determinant, so you include an extra sign change to compensate.

Next, you want to remove the 2 in the last row: R4 ← R4 + 2R2. This doesn't chnge the value of the determinant, so you get

This determinant is upper triangular, so you can calculate it as the product of the elements down the main diagonal:

.

You can use more than row operations. Here's another useful property of determinants.

For any square matrix A, det(AT) = det(A).

Proof: Omitted. (Uses the formal definition of the determinant).

This means that you can also use elementary column operations to evaluate determinants as well, since a column operation on A has the same effect as the corresponding row operation on AT.

Here's a table of the effect of the elementary column operations on a determinant.

Elementary column operation	Effect on the determinant
Ci ↔ Cj	changes the sign of the determinant
Ci ← cCi, c ≠ 0	multiplies the determinant by c
Ci ← Ci + kCj, j ≠ i	no effect on the determinant

A note about the second type of elementary row or column operation: this one's most useful if you think of it as factoring a number out of a row or column of a determinant instead of as multiplication. For example, factor a 3 out of column three in the following determinant:

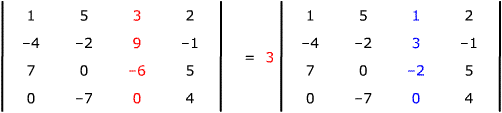
Caution: don't mix row and column operations in the same step. Here's a classic exam error – can you explain what the student did incorrectly?
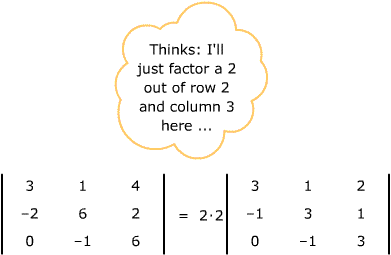